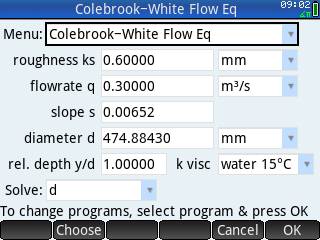
 This pipe calculator program calculates the unknown variable for Manning, Colebrook-White, Continuity (Q=), Area, Critical Flow, and shear stress equations for a circular pipe flowing partially full. The program uses the calculator’s unit functions, so the user must select the unit of the solve variable. The results are displayed on the calculator’s print terminal. To switch between programs, select the new program from the Menu on the INPUT screen and press the OK tab. To rerun the same program, press the Esc key to exit the terminal, and press the Enter key to rerun the program. Includes PDF documentation. |
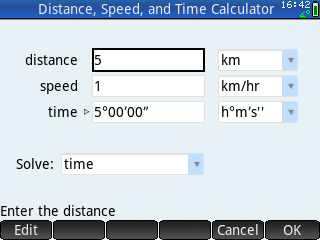A distance, speed and time calculator that uses the Units, MKSA, and CONVERT functions. Enter any two variables and solve for the third. When solving for the unknown variable, you need to specify the units of the unknown variable. When using h°m′s'' units for time, you need to enter the degrees, minute, and seconds symbols. One hour, 30 minutes and 45 seconds is entered as 1°30′45"
The lunar lander is 500 ft above the moon with a downward velocity of 50 ft/s and has 120 units of fuel. The height, velocity, and remaining fuel are displayed. The program will pause for up to 60 seconds. Enter the number of units of fuel you wish to burn during the next second, then press the Enter key. The new height, velocity and remaining fuel are displayed. The maximum amount of fuel you can burn at one time is 30 units. Adapted from the Rocket program in Basic Computer Games, MicroComputer Edition, 1978 by David H. Ahl.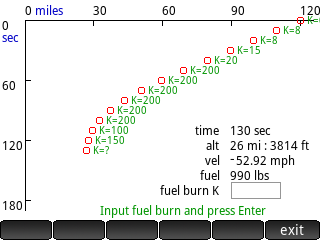
The lunar lander is 120 miles above the moon with a downward velocity of 3600 mph and has 16,000 pounds of fuel. The time, height, velocity, and remaining fuel are displayed. Enter the number of pounds of fuel (0, or between 8 and 200) you wish to burn per second during the next 10 seconds, then press the Enter key. The new height, velocity and remaining fuel are displayed, as well as a graph of the descent. The maximum amount of fuel you can burn at one time is 30 units. Adapted from Jim Storer's 1969 Lunar Lander simulator program that was written in FOCAL-69.
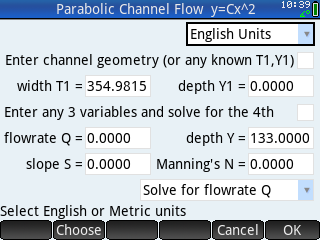Calculates the normal depth of a parabolic channel in the form of y = Cx^2, where C is the x^2 coefficient or curvature coefficient. The channel depth and width or any other known depth and width must be entered to describe the curvature of the parabola. Enter any three of the four variables (flow rate, depth, slope, and n) and solve for the fourth variable. The wetted perimeter P is calculated using the exact formula per Chow as redefined by Merkley. Includes comprehensive PDF documentation.
Calculate N, Q, S, Dia, or y/D for partially full pipes using Manning's Equation in English or Metric units. The program also computes the corresponding velocity. The depth of flow ratio, y/D, is solved by numerical analysis using the secant method. Where there are two solutions, only the first solution between 0 < y/D < 0.9381 is reported. When solving for the diameter, the calculated diameter and diameter rounded to a standard size are given. This program is a conversion of an old FORTRAN program that was printed in Schaum’s Solved Problems in Fluid Mechanics & Hydraulics, 1989.
Calculates the depth of flow in a composite gutter section using Manning’s equation modified for shallow or sheet flow using the HEC 22 (August 2013) equation that describes Q in terms of Sx, S, and T and not the equivalent equation that described Q in terms of Z, S, and d. Program assumes: (1) the curb face is vertical, (2) friction on the curb face is ignored, and (3) flow is contained in the street and gutter section, even if the water depth is above the height of the curb.
A simple trapezoidal channel calculator. Uses fsolve to solve Mannings and critical depth equations. For rectangular channels, use a side slope z=0. For triangular channels, use a bottom width b=0. Also calculates average shear stress.